
 |
| | |||||
| Part 1 | Magnetic resonance | Theory (I) | |||
| Part 2 | Magnetization | ||||
| Part 3 | Spectroscopy | ||||
| Fourier transformation | |||||
|
Nuclear magnetic resonance |
||
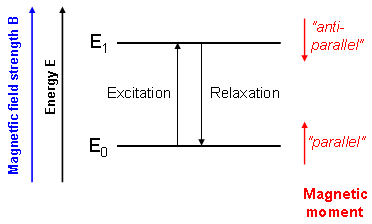 Figure 1 |
Nuclear magnetic resonance (NMR) methods are based on the physical properties of several nuclei that interact with magnetic fields thereby producing their own small magnetic moments. In the simplest case (e.g. for 1H-, 13C- or 31P nuclei), there are two orientations of these moments relative to the external magnetic field which can be thought of "parallel" and "anti-parallel" (Fig. 1).
These two states slightly differ in energy. Transitions between the associated energy levels can be induced using electromagnetic waves of appropriate frequency which is in this case radio frequency (RF). Thus, nuclei can be excited from parallel to anti-parallel spin states using an RF pulse. |
|
|
The excitation frequency associated with the energy level difference (ΔE = h·ν; h: Planck's constant) is called the Larmor frequency and is defined by the Larmor equation νL = γB/(2π) (γ: gyromagnetic ratio of the respective nucleus; B: applied magnetic field).
Often NMR scanners are not classified by their magnetic field strength but by the proton frequency calculated from γ(1H). For our experiments we use a 9.4T magnet which corresponds to 400 MHz, while 1.5T magnets with 64 MHz are commonly used for human applications (Fig. 2). After excitation by an RF pulse the system will relax to equilibrium which can be observed with an appropriate set-up. This "answer" of the probe can then be used for magnetic resonance spectroscopy or imaging. |
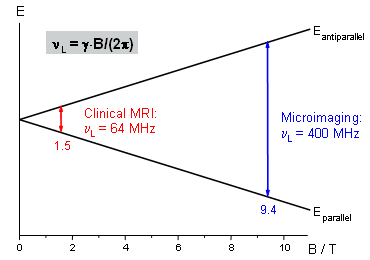 Figure 2 |
| Top |
Magnetization |
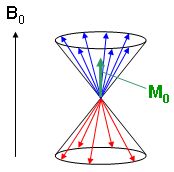 Figure 3 |
Summation of all individual magnetic moments results in a macroscopic magnetization vector that can be manipulated by means of magnetic resonance techniques. Due to quantum mechanics the spin axes and therefore the magnetization vectors of the individual nuclei are not fixed parallel or anti-parallel to the static magnetic field axis. Instead, they precess about this axis in two different ways (Fig. 3) and the expressions "parallel" and "anti-parallel" describe the average orientation of the vectors on the cone surfaces.
Fig. 3 illustrates a momentary situation with a statistically distributed portion of magnetization vectors moving on the cones. Summation over all spins leads to a magnetization vector M0 that is parallel to the static magnet field B0, since more spins are moving on the lower level cone (blue in Fig. 3) in the equilibrium situation. M0 can now be manipulated using an RF excitation pulse. |
| The simple case of a 90° excitation pulse is shown in Fig. 4, together with the axis definitions. During and after excitation the magnetization vector moves in a complicated way which can be simplified by using the following trick: referencing to the resonance frequency ν0 = γ·B0/(2π) which is identical to a rotation of the coordinate system about the z-axis with frequency ν0 leads to a simple rotation of the magnetization vector about the RF pulse (x-) axis onto the detector (y-) axis during excitation. |
|
Since at present, we are neglecting relaxation, the magnetization vector remains on the y-axis as long as the magnet field is exactly B0.
The vector position within the xy plane, the spin phase, can be manipulated by applying an additional magnetic field. Phase manipulations by magnetic field gradients are important for spatial encoding in MR imaging and will be discussed in more detail below. |
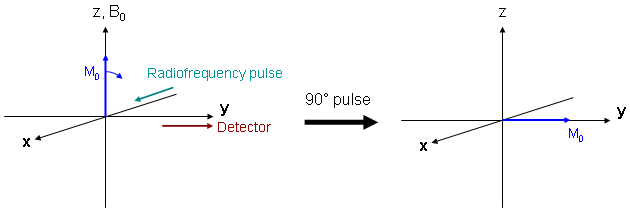 Figure 4 |
| Top |
NMR spectroscopy |
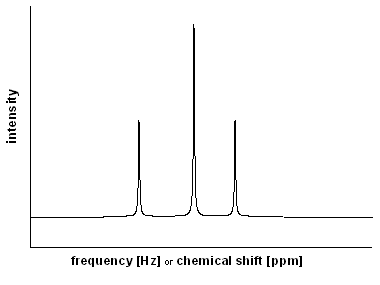 Figure 5 |
As can be seen from the Larmor equation, the difference between two energy levels of an NMR-active nucleus is directly proportional to the applied magnet field strength. Due to different environments and therefore different shieldings from the static magnetic field, the nuclei "feel" slightly different fields. Hence, all differently bound atoms of one species show slightly varying energy level differences very important for NMR spectroscopy. E.g., one can differentiate between methyl- or aromatic protons in 1H spectroscopy by measuring their different excitation energies. This technique is widely used for analysis of mixtures of materials, for quantitative analysis, or for structure determination.
The most intuitive approach to NMR spectroscopy would be to measure absorption while continously varying the excitation energy. As a result, a spectrum like that given in Fig. 5 would be recorded in which the intensity is given as a function of the excitation frequency (in Hz). Alternatively, it can be related to a reference frequency (ν0) resulting in the so-called chemical shift (in ppm = parts per million). |
|
In real experiments, neither the excitation frequency is tuned nor the absorption of the RF radiation is directly measured. Instead, all resonances within a defined frequency interval are synchronously excited and afterwards, the total emission of the probe is detected. The signal contains a mixture of individual frequencies which have to be identical to the excitation energies, since the properties of the nuclei did not change after excitation.
The M0 vector defined in the last section becomes smaller, since only spins with a resonance frequency exactly identical to the reference value are static. All other spins rotate in the xy plane with the respective difference frequency and contribute only partially to the total magnetization. An overlay of several frequencies is then detected which can be converted to an NMR spectrum. |
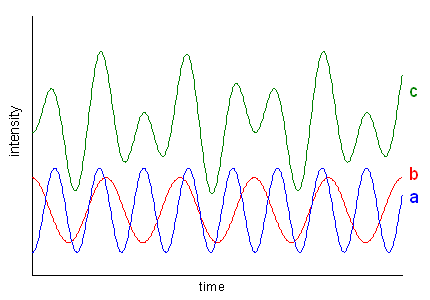 Figure 6 |
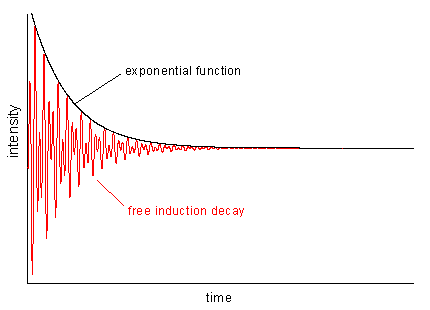 Figure 7 |
Such an overlay of frequencies is illustrated in Fig. 6 which shows two periodic functions (a and b) and their sum signal (c). In real life, the intensity of periodic motions, e.g. vibrations, descents more or less steeply (otherwise you would have a perpetual motion machine). The resulting function of time looks like the red curve in Fig. 7 which is the primary signal in NMR spectroscopy. This so-called FID (free induction decay) is the product of a periodic function containing a mixture of frequencies (as Fig. 6c) and an exponential decay function.
An FID contains all information necessary to obtain a spectrum like that in Fig. 5. All you need is a so-called Fourier transform operation that is briefly described in the following. |
| Top |
Fourier transformation |
| In order to transfer MR data from time (FID) to frequency domain (spectrum), we have to apply a mathematical operation called Fourier transformation (FT). Using FT all signals can be separated by their frequencies and the intensities in the spectrum are defined by the maximum FID amplitudes of the respective frequency components. Application of an FT to the signal in Fig. 6c leads to a two-line spectrum with more intensity on the higher frequency signal (6a). If there would be no signal damping in the FID, all lines in the spectrum were infinitely narrow. In real life, there is always relaxation leading to such a damping (cf. Fig. 7) and therefore, we always find line broadening in the spectra which depends on the exponential decay of the FID: the faster the decay, the broader the lines. |
|
|||