
 |
| | |||||
| Teil 1 | MR-Bildgebung | Theorie (II) | |||
| Teil 2 | Schichtselektion | ||||
| Teil 3 | Frequenzkodierung | ||||
| k-Raum | |||||
| Phasenkodierung | |||||
| Datenakquisition | |||||
|
MR-Bildgebung |
||
|
Auf der Basis der NMR-Spektroskopie läßt sich nun auch das Prinzip der Bildgebung relativ leicht verstehen. Statt die unterschiedlichen Resonanzfrequenzen zur Unterscheidung der verschiedenen Kerne zu verwenden, betrachtet man bei der Bildgebung nur identische Kerne, bei denen der Energieabstand bei gleichem Magnetfeld gleich groß ist. Da der menschliche Körper zu einem sehr hohen Anteil aus Wasser besteht, stellt diese Substanz den optimalen "Protonenspender" dar. Andere Protonen mit ähnlichen Resonanzfrequenzen (z.B. in Fett) sind ebenfalls in größeren Mengen im menschlichen Körper vorhanden und können die Bildqualität beeinflussen; zur Vereinfachung wollen wir aber davon ausgehen, daß nur eine Resonanzfrequenz existiert, so daß in einem Spektrum nur eine einzige Linie zu beobachten wäre.
Durch Einsatz von Magnetfeldgradienten in allen drei Raumrichtungen (Gx, Gy, Gz) kann man dann ortsabhängig unterschiedliche Resonanzfrequenzen erzeugen. Das resultierende Meßsignal (der FID) stellt dann wiederum eine Überlagerung unterschiedlicher Frequenzen dar, wobei die Intensitäten nach Fouriertransformation auf die Anzahl der sich an einem Ort befindlichen Wasserprotonen schließen läßt. Im MR-Bild werden diese unterschiedlichen Intensitäten dann durch entsprechende Helligkeitsunterschiede dargestellt. Die Schwierigkeit dieser Methode liegt nun darin, die Ortsinformation für die drei Raumrichtungen unterschiedlich zu verschlüsseln. Bei der 2D-Bildgebung (Tomographie) unterscheidet man zwischen Schichtselektion, Frequenz- und Phasenkodierung. Diese werden im folgenden beschrieben, wobei die Richtungen mit den kartesischen Achsen identifiziert werden. Prinzipiell ist die Wahl der Achsen natürlich beliebig, da durch Linearkombination der Gx,Gy,Gz beliebige orthogonale Gradienten erzeugt werden können. |
||
| Nach oben |
Schichtselektion |
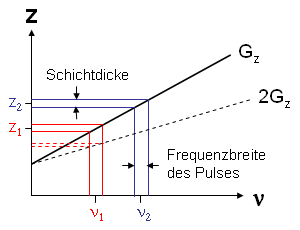 Abbildung 8 |
Die Tatsache, daß die Anregungsfrequenz direkt proportional zum angelegten Magnetfeld ist, kann man nun dazu nutzen, selektiv bestimmte Bereiche der Probe anzuregen. Ein Magnetfeldgradient in z-Richtung (Gz) bewirkt, daß sich B in dieser Richtung linear ändert und daß man mit einem Anregungspuls einer gewissen Frequenzbreite eine definierte Schicht anregt (Abb. 8). Durch Erhöhung des Gradienten (gestrichelte Linie) kann die Schichtdicke reduziert werden (für ν1 dargestellt), ebenso wie durch eine Verringerung der RF-Pulsbreite.
Das Gesamtmagnetfeld an einer Position zSS (SS = Slice Selection), bewirkt durch den Gradienten Gz, beträgt B0+zSS·Gz, woraus man mit Hilfe der Larmorgleichung die ortsspezifische Anregungsenergie bzw. -frequenz berechnen kann. Bei einer tomographischen MR-Aufnahme dient die Schichtselektion der Reduktion des 3D-Problems auf zwei Dimensionen. |
| Nach oben |
Frequenzkodierung |
|
Die Verschlüsselung der Ortsinformation muß nach der Schichtselektion nur noch in zwei Dimensionen erfolgen. Dabei unterscheidet man, ob der Gradient für die jeweilige Richtung vor oder während der Datenakquisition angewandt wird, wobei der erste Fall, die Phasenkodierung, weiter unten besprochen wird.
Im zweiten Fall, der sogenannten Frequenzkodierung, schaltet man einen Auslesegradienten GRO (RO = Readout), der entlang der Ausleserichtung ein linear variierendes Magnetfeld erzeugt. Somit ändert sich wegen der Proportionalität zwischen Magnetfeld und Frequenz auch letztere linear entlang dieser Richtung. Spins an unterschiedlichen Positionen emittieren daher Strahlung verschiedener Frequenzen, die nach der Fourier-Transformation unterschieden werden können. Die Intensität der Strahlung einer Frequenz läßt auf die Anzahl der Spins an der zugehörigen Achsenposition schließen.
Neben dieser anschaulichen Beschreibung der Wirkung des Auslesegradienten kann man die Frequenzkodierung auch analog zur (schwerer zu veranschaulichen) Phasenkodierung über die Manipulation der Variablen k beschreiben, wofür im folgenden kurz das Konzept des "k-Raums" vorgestellt wird. |
| Nach oben |
k-Raum |
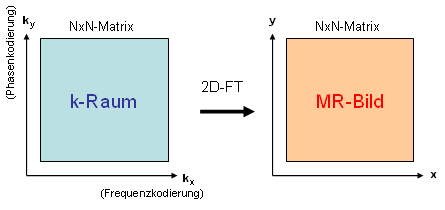 Abbildung 9 |
Bei "k-Raum" handelt es sich um die etwas mystische Bezeichnung für die Matrix, in der die Rohdaten abgespeichert werden, die dann durch Fourier-Transformation in ein Bild umgewandelt werden können (Abb. 9). Analog zur oben beschriebenen Transformation von der Zeit- in die Frequenzdomäne (s → 1/s) werden auch bei der Bildgebung zwei reziproke Größen betrachtet: m und 1/m. Ein tomographisches MR-Bild stellt nichts anderes als eine ortsabhängige Intensitätsverteilung dar und ist daher der Ortsdomäne zuzuordnen (m). Die Variable k beschreibt demnach die andere Domäne des Fourierpaares und besitzt die Dimension 1/m. |
|
Der Wert kx gibt an, wieviele Phasenzyklen pro Meter Abstand vom Nullpunkt der x-Achse ein Magnetisierungsvektor durch Wirkung des Magnetfeldgradienten (Gx) durchläuft. In Analogie zur Frequenz, die in Zyklen pro Zeiteinheit angegeben wird, spricht man hier von räumlicher Frequenz (spatial frequency).
Die Phasenänderung, die ein Magnetisierungsvektor erfährt, ist abhängig von der Stärke des angelegten Gradienten sowie von dessen Dauer. Bei einer sogenannten Pulssequenz (s.u.) werden neben den RF-Pulsen und dem Aquisitionsfenster auch die Gradientenamplituden in den einzelnen Richtungen angegeben. Die Größe von kx in Abb. 10 ist dabei proportional zur schraffierten Fläche, d.h., (für die dargestellte Rechteck-Pulsform) sowohl proportional zur Gradientenschaltdauer τx als auch zur (konstanten) Gradientenamplitude Gx. |
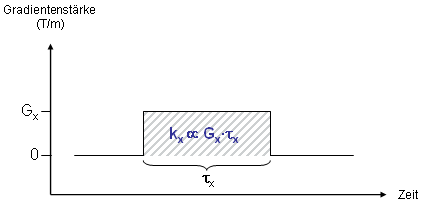 Abbildung 10 |
| Nach oben |
Phasenkodierung |
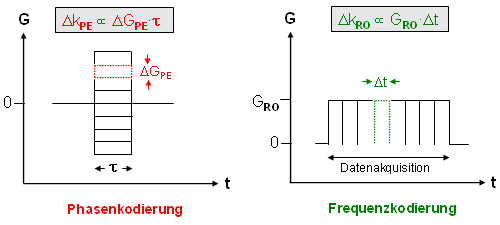 Abbildung 11 |
Wie bereits erwähnt wird der Phasenkodiergradient GPE (PE = Phase Encoding) bereits vor der Datenakquisition an- und wieder ausgeschaltet. Damit wird die (ortsabhängige) Phase der Spins und folglich kPE festgelegt. Für N Punkte in PE-Richtung benötigen wir genau N Werte für kPE, die man durch schrittweise Änderung von GPE erhält.
Folglich müssen N Akquisitionszyklen durchlaufen werden, bei denen GPE jeweils um ein konstantes ΔGPE verändert wird (Abb. 11, links). Mit einer konstanten Gradientendauer τ ergibt sich somit eine kontinuierliche Änderung von kPE um ΔkPE. Analog können wir die Änderung von k entlang des Auslesegradienten betrachten: GRO wird zwar konstant gehalten, doch eine kontinuierliche Veränderung von kRO wird hier über die Datenakquisition zu unterschiedlichen Zeitpunkten i·Δt (i=0..N-1) erreicht (Abb. 11, rechts). |
| Somit werden alle Werte von kRO während eines Akquisitionszyklus' erfaßt, so daß der Zeitaufwand für eine Messung im Wesentlichen durch die Anzahl der Phasenkodierschritte bestimmt wird. Bezogen auf den k-Raum wird in jedem Zyklus eine Zeile aufgenommen, während durch die Phasenkodierung ein Zeilenwechsel erfolgt. |
| Nach oben |
Datenakquisition |
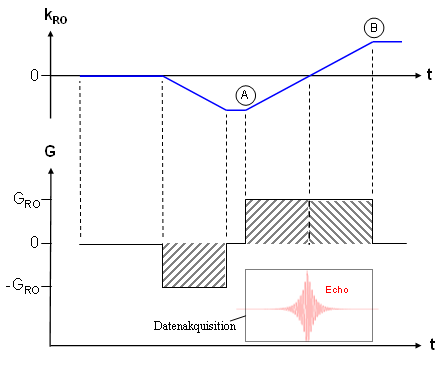 Abbildung 12 |
Im unteren Teil der Abb. 12 ist das mit dem positiven Auslesegradienten zusammenfallende Akquisitionsfenster mitsamt des Meßsignals, des sogenannten Echos, dargestellt.
Im oberen Teil des Bildes ist der Verlauf der Variablen kRO als Funktion der Zeit dargestellt, die innerhalb des genannten Zeitintervalls (zwischen A und B) vom minimalen zum maximalen Wert variiert wird. Der negative Startwert (A) wird dabei durch einen vorgeschalteten Gradienten erreicht, der entlang der Ausleseachse die Phase der Magnetisierung unterschiedlich verändert und somit netto zu einer Dephasierung der Gesamtmagnetisierung (ursprünglich M0) führt. Bei Anlegen des positiven Gradienten werden diese Phasenmanipulationen rückgängig gemacht, bis bei Gleichheit von negativer und positiver Fläche der Ursprungszustand wiederhergestellt ist und die gesamte Probe rephasiert ist. Zu diesem Zeitpunkt ist kRO=0 und das Echo durchläuft sein Maximum. Anschließend bewirkt der Gradient wiederum eine Dephasierung des Signals. |
|
Abb. 13 verdeutlicht, wie man sich negative bzw. positive Gradienten vorstellen kann: entlang der Ausleserichtung wird die Magnetfeldkomponente in B0-Richtung linear variiert, wobei der Nullpunkt normalerweise mit dem Zentrum des Objekts (x=0) zusammenfällt.
Bei einem positiven Gradienten ist dabei für x<0 ein B0 entgegengerichtetes Magnetfeld wirksam, für x>0 ein parallelgerichtetes. Bei x=0 ist der Magnetisierungsvektor somit statisch, während sich die benachbarten Spins symmetrisch aber in unterschiedliche Richtungen innerhalb der xy-Ebene bewegen. Ein negativer Gradient kehrt diese Verhältnisse exakt um (eingezeichnete Pfeile). |
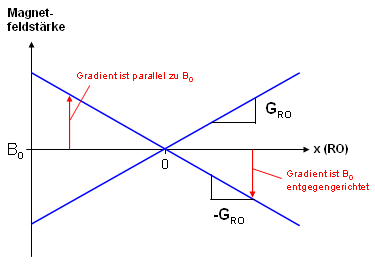 Abbildung 13 |
| Nach oben |
|
|||