
 |
| | |||||
| Teil 1 | Relaxation | Theorie (III) | |||
| Teil 2 | Pulssequenzen | ||||
| Teil 3 | Spinechos | ||||
| Bildgebungsparameter | |||||
| Spezielle Anwendungen | |||||
| Literaturhinweise | |||||
|
Relaxation |
||
|
Bei Betrachtung der Relaxation, die unvermeidbar stattfindet, wenn das untersuchte System durch einen RF-Puls aus dem Gleichgewicht gebracht wurde, muß man zwei unterschiedliche Prozesse betrachten: die T1- und die T2-Relaxation. Erstere bezeichnet man dabei auch als Spin-Gitter-Relaxation, da es Wechselwirkungen mit der Umgebung (dem "Gitter") sind, die eine Rückkehr der angeregten Spins in den Grundzustand ermöglichen. Die freiwerdende Energie kann dabei von Molekülen der Umgebung in Form kinetischer Energie übernommen werden. Aus der damit verbundenen vermehrten Besetzung des energieärmeren Zustands resultiert ein Wiederaufbau der Magnetisierungskomponente in B0-Richtung, der sogenannten Longitudinalmagnetisierung, die sich M0 annähert (vgl. Abb. 3).
Bei der T2-Relaxation (Spin-Spin-Relaxation) kommt es hingegen zu keiner Änderung der Energie, sondern es tritt lediglich eine Veränderung der Phasen einzelner Spins ein, bewirkt durch die aus Fluktationen der Umgebungsmoleküle hervorgehenden Magnetfelder. Aus der damit verbundenen Dephasierung folgt eine Abnahme der Magnetisierungskomponente in der xy-Ebene (Transversalmagnetisierung Mxy) und somit ein Signalabfall gemäß Abb. 7. Die beschriebenen Mechanismen sind schematisch in Abb. 14 dargestellt. |
||
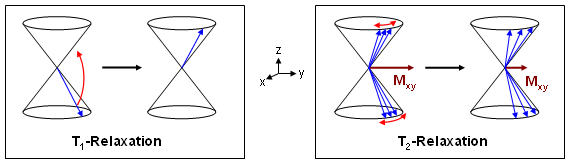 Abbildung 14 |
Man sieht, daß die Energieänderung bei der T1-Relaxation ohne Änderung der Phase (Komponente innerhalb der xy-Ebene) abläuft, während bei der T2-Relaxation keine Energie- sondern lediglich eine Phasenänderung zu beobachten ist. Somit sind die beiden Prozesse unabhängig voneinander, und ihr zeitlicher Verlauf kann separat beschrieben werden, auch wenn beide Prozesse parallel ablaufen und ein kompliziertes Verhalten des Gesamtmagnetisierungsvektors (Änderung von Richtung und Länge) während der Relaxationsphase bewirken. |
|
Die zeitlichen Verläufe der T1- und T2-Relaxation sind für Fett, Blut und Wasser in Abb. 15 dargestellt, wobei t=0 den Zeitpunkt unmittelbar nach einer 90°-Anregung (ausgehend von einer relativen Magnetisierung von 1) darstellt. Wie aus den angegebenen Gleichungen ersichtlich, handelt es sich um exponentielle Verläufe, die je nach Größe der Zeitkonstanten T1 bzw. T2 für verschiedene Substanzen recht unterschiedlich aussehen.
Z.B. sind beide Konstanten für Wasser vergleichsweise hoch, so daß sowohl der Wiederaufbau der Longitudinal- als auch die Dephasierung der Transversalmagnetisierung langsam verlaufen. Beim Fett hingegen laufen beide Relaxationsprozesse deutlich schneller ab. |
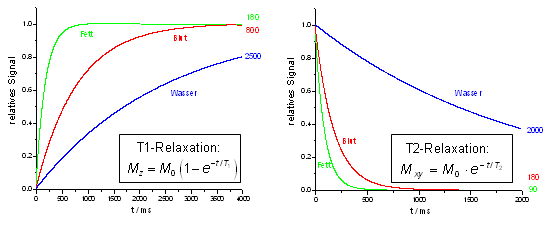 Abbildung 15 |
| Alle bisher angesprochenen Relaxationsmechanismen sind bei gegebener Temperatur und Molekülumgebung schwer zu beeinflussen. Dephasierungsprozesse infolge eines inhomogenen Magnetfeldes, die manuell minimiert werden können (Shimming), werden als Variante der T2-Relaxation mit T2* bezeichnet. Da T2* normalerweise deutlich kleiner als T2 ist, wird der Signalabfall eines FIDs (vgl. Abb. 7) fast ausschließlich durch T2*-Effekte bestimmt. Allgemein gilt T1>T2>T2*. |
| Nach oben |
Pulssequenzen |
|
Als Pulssequenz bezeichnet man die Hardwareimplementierung der Komponenten, die für die Anregung, Kodierung und Datenakquisition benötigt werden. Sie wird mit Hilfe eines Schemas beschrieben, in dem sämtliche RF-Pulse, Gradienten sowie das Akquisitionsfenster in Abhängigkeit von der Zeit für das kleinste sich wiederholende Zeitintervall dargestellt sind. Dies soll am Beispiel von Abb. 16 näher erläutert werden, in der die Pulssequenz für ein einfaches 2D-Gradientenecho dargestellt ist.
In der oberen Spur (RF) sieht man den Anregungspuls, dessen Pulswinkel α variabel und meist kleiner als die in Abb. 4 dargestellten 90° ist (Erklärung s.u.). Die drei Spuren darunter repräsentieren die Schaltungen der einzelnen Gradienten. |
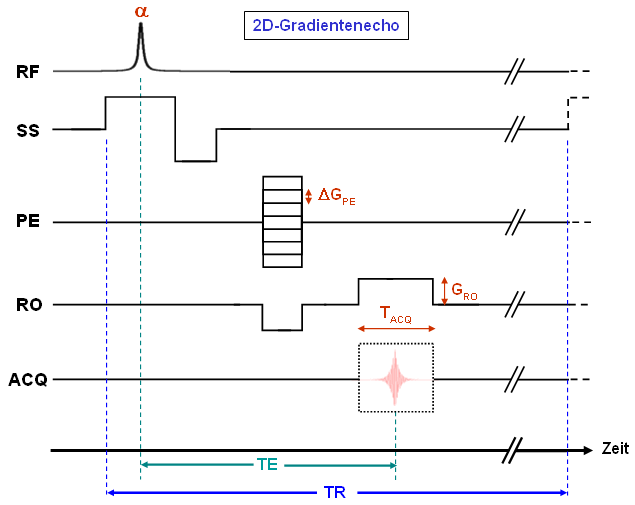 Abbildung 16 |
Die Schichtselektion (SS) wird durch gleichzeitiges Schalten mit dem RF-Puls realisiert, der nur Spins innerhalb eines definierten Intervalls des Gesamtmagnetfeldes (B0+zSS·GSS) anregen kann. Da innerhalb dieser Schicht durch den Gradienten unterschiedliche Phasen generiert werden, folgt ein Rephasierungsgradient mit entgegengesetztem Vorzeichen. Schließlich werden Phasenkodier- (PE) und Dephasierungsgradient in Ausleserichtung (RO) geschaltet, bevor, zeitgleich mit der Datenakquisition, GRO wirksam wird.
Es sei bemerkt, daß GPE und der negative Gradient in Ausleserichtung auch zeitlich getrennt oder gleichzeitig mit der Rephasierung des Schichtselektionsgradienten geschaltet werden können, da die einzelnen Richtungen orthogonal zueinander sind und Phasenmanipulationen in diesen unabhängig voneinander durchgeführt werden können. Diese Details sind abhängig von der Implementierung oder auch von den durch den Benutzer gewählten Zeitparametern, während auf entscheidende Unterschiede zwischen den vorgestellten Sequenzen im Text explizit hingewiesen wird. |
|
Das in Abb. 16 dargestellte Zeitschema deckt die Aufnahme einer Zeile des k-Raums ab und wird in fast identischer Weise bis zum Ende der Messung wiederholt. Der RF-Puls sowie die Gradienten in SS- und RO-Richtung bleiben dabei unverändert; lediglich der Phasenkodiergradient wird um einen definierten Betrag ΔGPE geändert, was in der Pulssequenz durch eine der Abb.11 (links) entsprechende Darstellung von GPE angedeutet wird. |
|
In der Abbildung sind zwei wichtige Zeitparameter mit eingezeichnet: die Echozeit (TE) und die Repetitionszeit (TR). TE definiert die Zeit zwischen der Anregung und dem Maximum des Gradientenechos, TR die Dauer eines Phasenkodierzyklus'. Beide Größen können vom Benutzer als Meßparameter vorgegeben werden (s.u.) und dienen z.B. der Erzeugung bestimmter Kontraste aufgrund unterschiedlicher Relaxationszeiten zweier Stoffe. TR kann dabei durch Verlängerung des Intervalls zwischen Akquisitionsende und erneuter Anregung beliebig groß gewählt werden, was durch die Achsenunterbrechung angedeutet werden soll.
Die meisten Pulssequenzen stellen Varianten der Gradientenecho- oder der Spinechomethode dar, deren (2D-) Sequenz in Abb. 17 gezeigt ist und deren Prinzip im folgenden Abschnitt beschrieben wird. |
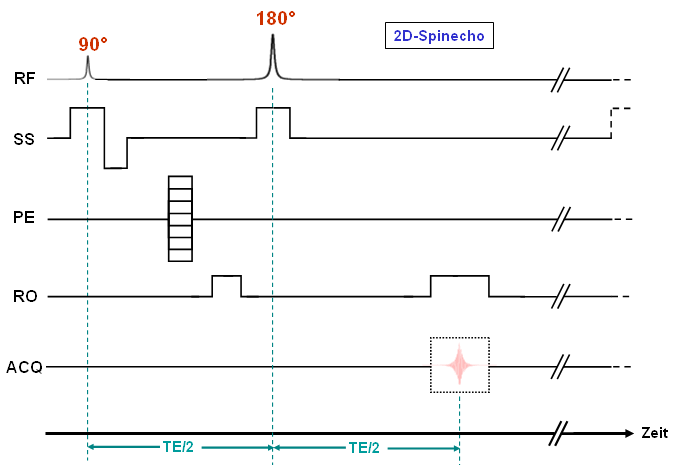 Abbildung 17 |
| Nach oben |
Spinechos |
|
Wie aus Abb. 17 ersichtlich, werden für einen Spinecho-Zyklus zwei RF-Pulse benötigt, wobei der erste der Anregung und der zweite der sogenannten Refokussierung dient. Während beim Gradientenecho der Pulswinkel (α) meist kleiner als 90° ist, verwendet man hier für die Anregung 90° und benötigt darüber hinaus für die Refokussierung einen exakten 180°-Puls. |
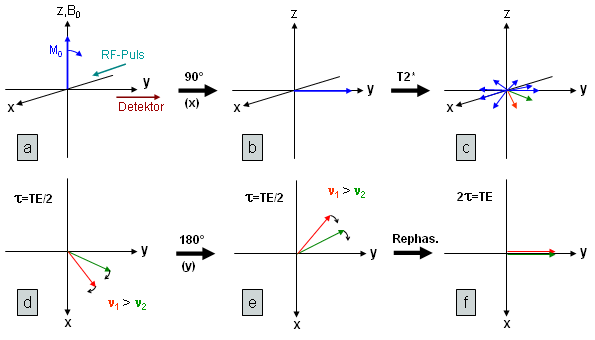 Abbildung 18 |
Um dies zu verstehen, schauen wir auf Abb. 18, in der die Anregung (a,b) und die darauffolgende Auffächerung der Transversalmagnetisierung (c) durch Magnetfeldinhomogenitäten (T2*-Relaxation), die den schnellen Abfall des FIDs hauptsächlich bewirkt (s.o.), dargestellt sind. In (d) sind die Vektoren für zwei der mit unterschiedlichen Frequenzen rotierenden Spingruppen zu einem bestimmten Zeitpunkt τ nach Anregung abgebildet. Der Refokussierungspuls (zur Zeit τ=TE/2, vgl. Abb. 17) soll im gezeigten Beispiel aus der y-Richtung eingestrahlt werden und bewirkt somit eine 180°-Rotation um diese Achse (e). Dieser Puls verändert die durch das lokale Magnetfeld vorgegebenen Rotationsgeschwindigkeiten nicht (die Richtungen sind durch die Differenz zur Referenzfrequenz gegeben und bleiben daher ebenfalls gleich), so daß sich jetzt beide Vektoren auf die y-Achse zubewegen und der schnellere nun "hinter" dem langsameren liegt. Nach einer Zeitspanne, die wiederum TE/2 beträgt, fallen die Vektoren wieder zusammen und sind somit auf der Detektorachse refokussiert (f). |
|
Dieses Prinzip läßt sich auf beliebig viele Vektoren übertragen, so daß alle auseinanderlaufenden Teilmagnetisierungen wieder zusammengeführt werden und ein sogenanntes Spinecho bilden.
Während Gradientenechos meist kurz nach der Anregung durch die entsprechenden Gradienten und somit De- sowie Rephasierung innerhalb der Abklingkurve des FIDs erzeugt werden, kann beim Spinechoverfahren eine Refokussierung lange nach Abklingen des FIDs erreicht werden. Solange die Spins demselben lokalen Magnetfeld ausgesetzt sind, läßt sich diese Prozedur wiederholen, bis das Signal aufgrund von T2-Effekten vollständig abgeklungen ist. In Abb. 19 ist dies am Beispiel zweier Echos dargestellt, deren Maximum im Zuge des T2-bedingten exponentiellen Signalabfalls abnimmt. Effekte, die eine T2-Relaxation bewirken, laufen extrem schnell ab, so daß sich die Umgebung der Spins ständig ändert und eine Refokussierung in diesem Fall unmöglich ist. |
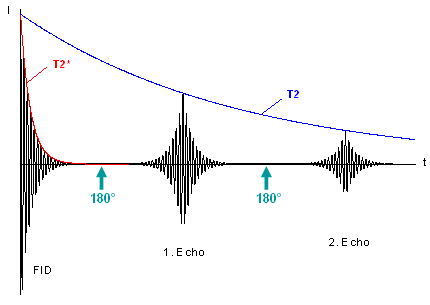 Abbildung 19 |
| Zum Schluß noch einige Anmerkungen zur Spinechosequenz in Abb. 17: Damit der 180°-Puls auf dieselbe Schicht angewandt wird, in der zuvor die Anregung erfolgt ist, muß der Schichtselektionsgradient wiederum gleichzeitig mit dem RF-Puls angeschaltet werden. Eine nachfolgende Rephasierung ist nicht notwendig, da GSS symmetrisch zum 180°-Puls gelegen ist und sich somit Phasenverschiebungen vor und nach dem Puls, analog zu der in Abb. 18d-f dargestellten Situation, ausgleichen. Aus demselben Grund ist der Dephasierungsgradient in Ausleserichtung positiv. |
| Nach oben |
Bildgebungsparameter |
| Da für die Bildgebung eine Vielzahl an Parametern existiert, die zum Teil auch spezifisch für die verwendete Pulssequenz sind, können hier nur einige ausgewählte angesprochen werden. Eine wichtige Größe ist der bereits mehrfach angesprochenen Pulswinkel (α), mit dem Intensität bzw. Kontrast entscheidend beeinflußt werden. |
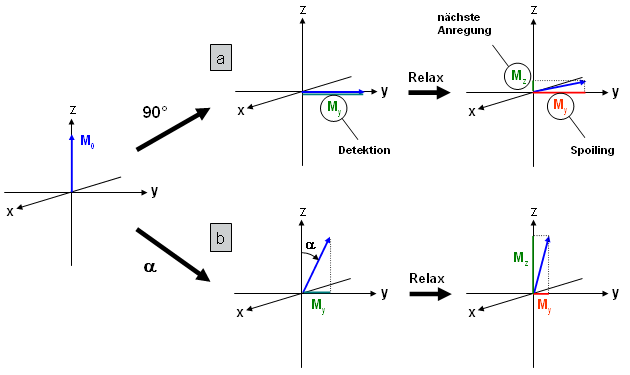 Abbildung 20 |
Dazu betrachten wir die 90°-Anregung und anschließende Relaxation am Beispiel eines Gradientenechos in Abb. 20a. Wie bereits erwähnt kann diese Sequenz mit kurzen Repetitionszeiten durchgeführt werden, so daß die Zeit zwischen Datenakquisition und erneuter Anregung (für den nächsten Phasenkodierschritt) recht kurz ist und nur ein geringer Teil der Longitudinalmagnetisierung relaxiert ist (Mz, grün).
Die verbleibende Transversalmagnetisierung wird bei Standardanwendungen meist durch sogenannte Spoilergradienten eliminiert und somit nicht weiter genutzt (My, rot). Für den zweiten und alle nachfolgenden Anregungen steht folglich nur ein sehr kleiner Teil der anfänglichen Magnetisierung zur Verfügung, woraus eine geringe Intensität im MR-Bild resultiert. |
|
Abb. 20b zeigt die Situation bei Verwendung eines kleineren Pulswinkels. Hier wird zwar beim ersten Puls eine geringere Magnetisierungskomponente My (sin(α)·M0, grün) registriert, aber nach der Relaxation ist die für die nachfolgenden Pulse verwendete Menge an Mz beträchtlich größer als im Fall der 90°-Anregung. Somit erreicht man durch Verwendung eines Pulswinkels α<90° (geringere Dauer oder Intensität des RF-Pulses) eine höhere Intensitätsausbeute. Für eine bestimmte Substanz existiert zu jedem TR ein optimaler Pulswinkel (Ernstwinkel genannt). Die beschriebene Gradientenechomethode bezeichnet man als FLASH- (Fast Low Angle SHot) oder GEFI-Sequenz (Gradient Echo Fast Imaging). |
|
In manchen Fällen steht nicht die maximale Intensitätsausbeute sondern die Erzeugung eines Kontrasts zwischen zwei benachbarten Substanzen im Vordergrund. So kann man z.B. durch eine kurze TR eine T1-Gewichtung erreichen, da kurz nach der Anregung die Longitudinalrelaxation für die einzelnen Substanzen sehr unterschiedlich verlaufen kann.
In Abb. 21 sind oben die T1-Kurven für Blut und Fett dargestellt, die die Longitudinalmagnetisierung relativ zum Ausgangswert (M0) nach einem 90°-Puls repräsentieren. Die zusätzlich eingezeichnete Differenzkurve zeigt an, daß ein maximaler Intensitätsunterschied bei einer relativ kurzen TR von etwa 300 ms zu finden wäre. Für t=T1 (gestrichelte Linien) ist die Transversalmagnetisierung jeweils auf den Anteil 1-1/e (63 %) angewachsen; um T1-Gewichtung (fast) vollständig auszuschließen, sollte eine TR=5·T1 verwendet werden, im Falle des Blutes also 4 Sekunden. Gibt man den Spins in der Transversalebene gleichzeitig möglichst wenig Zeit zur Dephasierung, so bekommt man protonendichtegewichtete (PD = Proton Density) Bilder, was nichts anderes bedeutet, als daß man dort am meisten Signal erhält, wo sich die höchste Anzahl an Protonen befindet. Bei verlängerter Echozeit kann man hingegen die unterschiedlichen T2-Eigenschaften der Substanzen nutzen, um Kontraste zu erzeugen. Abb. 21 (unten) zeigt die T2-Kurven für Blut und Fett sowie die Differenzkurve, die ein Maximum bei ca. 125 ms aufweist, was eine recht lange Echozeit darstellt. Für t=T2 sind die Signale jeweils auf den Anteil 1/e (37 %) abgefallen. Nebenbei bemerkt lassen sich T2-gewichtete Bilder mit der FLASH-Sequenz nicht erzeugen, da hier die T2*-Relaxation einen schnellen Signalabfall induziert. Erst durch Refokussierung (Spinecho) kann man entsprechend lange Echozeiten erreichen. |
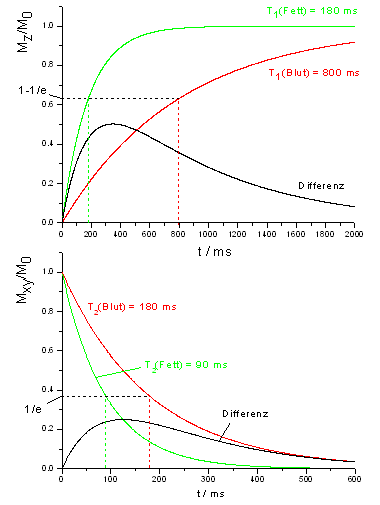 Abbildung 21 |
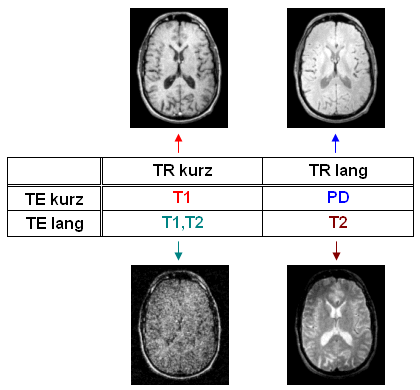 Abbildung 22 |
Das Gesagte ist in Abb. 22 tabellarisch zusammengefaßt, wobei die dargestellten Bilder die jeweiligen Gewichtungen eindrucksvoll repräsentieren. Für die Kombination kurze TR/lange TE kann keine eindeutige Gewichtung erreicht werden; da aber beide Parameter in dieser Form zu einer Signalabnahme führen, spielt die genannte Kombination aufgrund des daraus resultierenden schlechten Signal-Rausch-Verhältnisses (SNR = Signal to Noise Ratio) in der Praxis keine Rolle.
Die bisher behandelten drei Parameter sind, zusammen mit einigen anderen, in Tab. 1 zusammengestellt. Das Gesichtsfeld (FOV = Field Of View) ist hier für die beiden Richtungen eines tomographischen Schnittes einzeln aufgeführt; in der Literatur findet man jedoch oft eine Angabe als Produkt aus den zwei (2D) bzw. drei (3D) Längen des FOV. Im 3D-Fall entspricht die Länge der dritten Dimension der Schichtdicke eines 2D-Bildes, wobei man durch zusätzliche Phasenkodierschritte (die man hier als Partition Encoding bezeichnet) auch in dieser Richtung eine räumliche Auflösung erhält. Mit Hilfe des Quotienten FOV/Punktzahl kann man für jede Richtung die Pixel- (2D) bzw. Voxellänge (3D) angeben, die die räumliche Auflösung definiert. Dabei muß die Punktzahl der Rohdaten nicht unbedingt derjenigen des resultierenden Bildes entsprechen. Vielmehr kann die Größe des k-Raums durch Auffüllen mit Nullen (Zerofilling) erhöht werden, was nach Fourier-Transformation zu einer komplexen Mittelung der Pixelintensitäten führt. Die damit verbundene Interpolation der Daten liefert uns dann eine scheinbar erhöhte Auflösung. |
|
|
Die Anzahl der Mittelungen (NS = Number of Scans) erhöht man, um das SNR zu verbessern. Leider ist die Meßzeit proportional zur Anzahl der gemittelten Scans, während die SNR sich lediglich um die Wurzel aus NS erhöht.
Die Bandbreite entspricht der Abtastrate während der Datenakquisition. Deren Kehrwert entspricht somit der Zeit Δt zwischen der Aufnahme zweier Datenpunkte, woraus sich durch Multiplikation mit NRO auch die Breite des Akquisitionsfensters (TACQ) bestimmen läßt. Die Gesamtmeßzeit zur Aufnahme eines 2D-Datensatzes läßt sich nach Ttot = NS·NPE·TR bestimmen. Bei einem 3D-Scan muß diese noch mit der Anzahl der Partition-Encoding-Schritte multipliziert werden. |
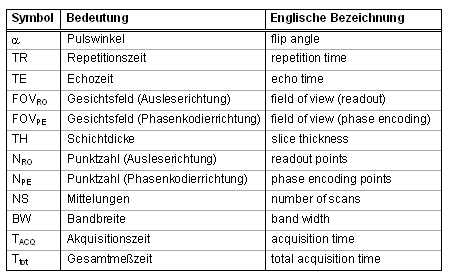 Tabelle 1 |
| Nach oben |
Spezielle Anwendungen |
| Alle Bildgebungsverfahren lassen sich im Prinzip in Gradientenecho- und Spinechoverfahren (vgl. Abb. 16 und 17) einteilen. Dennoch gibt es unzählige Varianten, die z.T. hochspezialisiert auf die Messung bestimmter physikalischer und chemischer Eigenschaften sind. Methoden wie CSI oder die diffusionsgewichtete Bildgebung, die wir in unserem Institut anwenden, sollen an dieser Stelle näher besprochen werden. |
| CSI (Chemical Shift Imaging) |
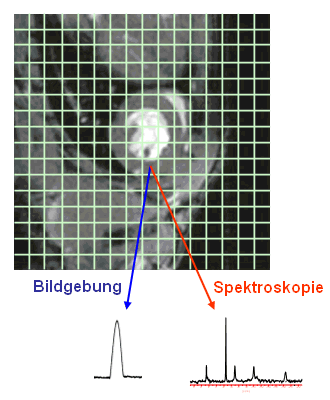 Abbildung 23 |
CSI stellt eine Kombination aus MR-Bildgebung und NMR-Spektroskopie dar, weshalb man auch von "spektroskopischer Bildgebung" spricht.
Beim MRT-Bild kann man jedem Pixel ein Signal zuordnen, das sich nach 2D-Fourier-Transformation aus den Rohdaten ermitteln läßt. Die Größe des Signals ist proportional zur Intensität, also zur Graustufe, in der das Pixel im tomographischen Bild dargestellt wird. Beim CSI wird nun jedem Pixel anstatt eines einzelnen Signals ein NMR-Spektrum zugeordnet, wobei die Rasterung normalerweise wesentlich gröber ist, d.h., die Anzahl der Pixel nimmt stark ab. Dies soll anhand der Abb. 23 näher erläutert werden, die das tomographische 1H-MR-Bild eines Mäuseherzens zeigt, über das ein 16×16-Raster gelegt wurde. Das Herzbild besteht aus 256×256=65536 Pixeln, so daß sich in einem hellgrünen Quadrat insgesamt 256 Pixel (mit individuellen Graustufen) befinden. Für das gesamte Quadrat erhalten wir bei Anwendung der CSI-Methode ein Spektrum (abgebildet ist hier ein 31P-Spektrum mit den Signalen für anorganisches Phosphat, Phosphocreatin und Adenosintriphosphat), so daß der resultierende Datensatz aus 256 Spektren besteht. Eine solche Ansammlung von Spektren kann z.B. dazu genutzt werden, Aussagen über den Energiestatus eines Mäuseherzens in vivo zu erhalten. Dabei kann man Signale von außerhalb des Herzens weitgehend eliminieren und gegebenenfalls regionale Unterschiede innerhalb des Herzens detektieren. |
|
Um Spektren erhalten zu können, darf die im FID oder Echo enthaltene Frequenzinformation nicht (wie bei der Bildgebung üblich) der Ortsverschlüsselung dienen, d.h., während der Datenakquisition wird kein Auslesegradient geschaltet (vgl. Abb. 24). Statt der Frequenzkodierung wird also wie bei der NMR-Spektroskopie ein FID registriert, dessen Frequenzkomponenten durch Kerne mit unterschiedlicher Umgebung erzeugt werden.
Keinen Auslesegradienten zu verwenden bedeutet aber, daß die gesamte Ortskodierung über Phasenkodierschritte ablaufen muß, so daß eine N×N-Matrix N2 Meßzyklen erfordert. Dies ist einer der Gründe, warum die Matrixgröße bei CSI-Messungen gegenüber Standardbildgebungsdatensätzen deutlich reduziert ist. Beim (2D-)CSI erhält man dreidimensionale Datensätze, von denen zwei Dimensionen auf die phasenkodierten Ortskoordinaten und eine auf die spektrale Komponente entfallen. |
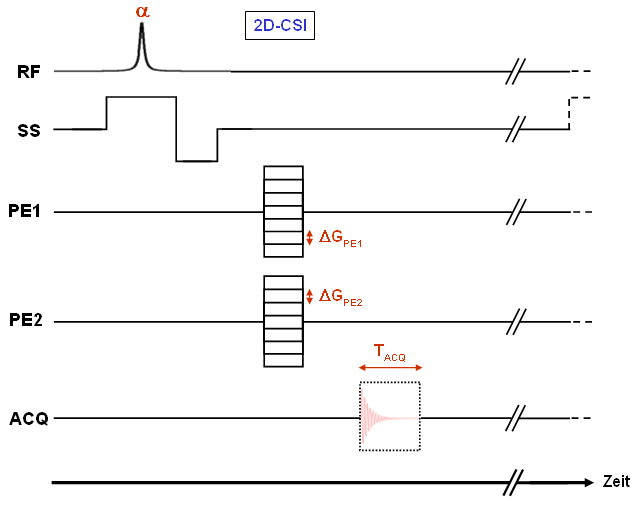 Abbildung 24 |
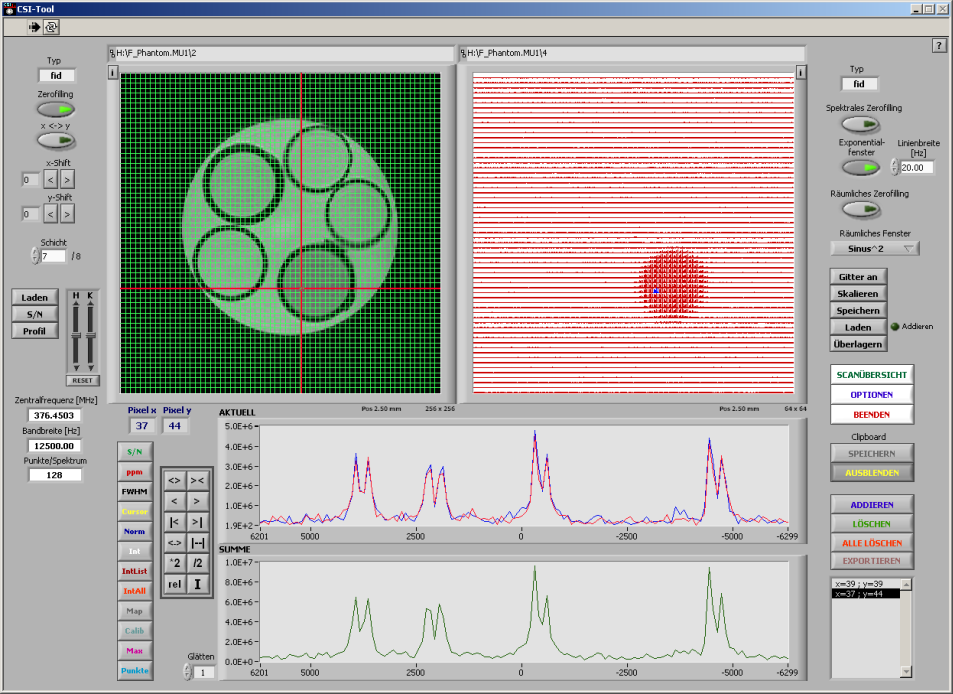 Abbildung 25 |
| Durch Verwendung eines doppelt abgestimmten Probenkopfes kann man ohne Umbau 1H- und 31P-Messungen derselben Schicht unmittelbar hintereinander durchführen. Somit erhält man zuverlässig die anatomische Referenz zu den 31P-Spektren wie in Abb. 25 zu erkennen ist. In diesem Screenshot des in unserem Institut entwickelten "CSI-Tools" sieht man in den beiden oberen Graphen den tomographischen Schnitt durch den linken Ventrikel des Mäuseherzens (links) sowie die Spektren für die durch die grünen Gitterlinien angedeuteten Teilbereiche (rechts). Mit Hilfe der Software können nun beispielsweise die Spektren verschiedener Bereiche addiert und/oder integriert werden (nähere Informationen zum Auswerteprogramm finden Sie hier). |
| Diffusionsgewichtete Bildgebung |
| Diffusionsgewichtete (Spinecho-)Sequenzen sind in medizinischen Anwendungen recht weit verbreitet, da man mit ihnen beispielsweise Infarktbereiche im Gehirn schon zu einem sehr frühen Zeitpunkt erkennen kann (Schlaganfalldiagnostik). Sie sind verbunden mit einer Signalabnahme an Orten starker Diffusion bzw. -zunahme (relativ zu anderen Bereichen) bei eingeschränkter Bewegungsfreiheit. |
|
Um das Prinzip der Diffusionsgewichtung zu erläutert, betrachten wir zuerst einmal einen bipolaren Puls wie in Abb. 26a, der z.B. in eine Gradientenechosequenz integriert werden kann. Alle Spins erhalten durch den positiven Gradienten eine ortsabhängige Phasenänderung, deren Ausmaß von der Fläche des Gradientenpulses (hier G·δ) abhängt. Durch den sich unmittelbar anschließenden negativen Puls gleicher Fläche wird der Effekt des ersten Pulses kompensiert (die Magnetisierung wird refokussiert), vorausgesetzt, die Spins befinden sich noch am selben Ort.
Haben sie sich dagegen in der Zwischenzeit (in Richtung des Gradienten) bewegt, so kann der Ursprungszustand nicht exakt wiederhergestellt werden, und ein Intensitätsverlust ist die Folge. Je größer das Ausmaß der Diffusion, desto größer ist die Menge der nicht refokussierten Spins und desto größer wird daher die Signalabnahme. Relativ zu den Orten hoher Diffusion erscheinen die Bildpixel hell, wenn an den entsprechenden Stellen die Bewegung eingeschränkt ist, da dann kaum Intensitätsverlust zu verzeichnen ist (im Vergleich zum Bild ohne Bipolarpuls). Das Ausmaß des Signalverlustes durch Diffusion läßt sich durch den exponentiellen Ausdruck S=S0·exp(-b·D) beschreiben, wobei S0 dem Signal ohne Gradienten (bei gleicher Echozeit!) und D der Diffusionskonstante entspricht, während b durch die Meßparameter bestimmt ist. Für den in Abb. 26a dargestellten Puls läßt sich b nach b = ²/3·γ2·G2·δ3 berechnen. Sowohl eine Erhöhung von G als auch von δ haben somit einen höheren Signalverlust zur Folge. |
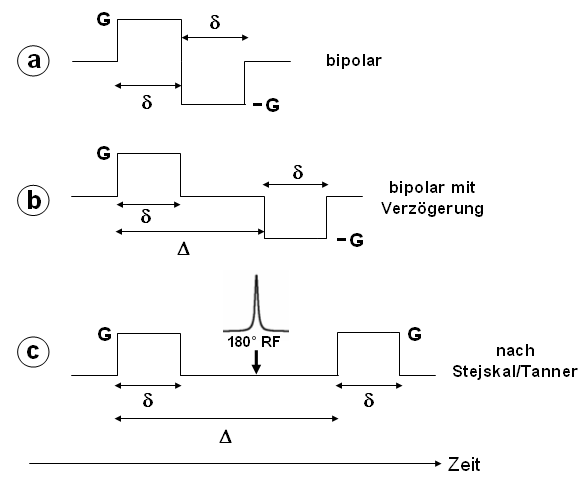 Abbildung 26 |
| Die Flexibilität der Sequenz läßt sich durch Einführung einer Verzögerung Δ (vgl. Abb. 26b) erhöhen, die den Abstand der beiden Gradientenpulse definiert. Auch ihre Erhöhung verstärkt die Signalabnahme bei Diffusion. Eine Erhöhung von Δ verlangt aber auch eine vergleichsweise große Echozeit, was für Gradientenechosequenzen durch schnellen, T2*-bedingten Signalabfall zu einem kleinen S0 führt. Daher verwendet man meist Spinechosequenzen, bei denen der Refokussierungspuls nun von Gradienten (gleichen Vorzeichens!) flankiert ist (Abb. 26c). Diese Sequenz geht auf Stejskal und Tanner zurück (J Chem Phys 42, 288 (1965)), und die Gleichung für b lautet, ebenso wie die für den bipolaren Puls mit Verzögerung: |
| b = γ2·G2·δ2(Δ–¹/3δ) |
| Mit dieser Sequenz kann nun entweder ein Kontrast zwischen Bereichen niedriger und hoher Diffusion erzeugt werden (diffusionsgewichtete Bildgebung), oder man ermittelt für jedes Pixel eine Diffusionkonstante (da man in vivo eingeschränkter Diffusion ausgesetzt ist, spricht man von einer "scheinbaren Diffusionskonstante" bzw. im Englischen Apparent Diffusion Constant, kurz ADC) und stellt diese im Bild da (ADC-Map). |
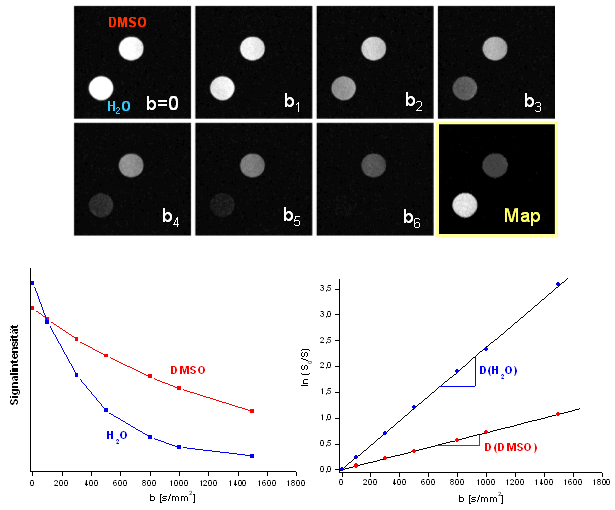 Abbildung 27 |
Dies ist in Abb. 27 dargestellt, in dem links oben ein Spinecho-Bild (b=0) zweier Phantome, von Dimethylsulfoxid (DMSO) und von Wasser, zu sehen ist. In den als b1 bis b6 bezeichneten Bildern sieht man die Auswirkung der Diffusionsgradienten, wobei G und somit auch b sukzessive erhöht wurden (bei konstanten Zeitkonstanten δ und Δ). Entsprechend der exponentiellen Signalabfälle, die unten links dargestellt sind, nimmt die Intensität des Wassers bei Zunahme von b stärker ab, und der Kontrast zwischen beiden Substanzen wird verstärkt. Aus den Exponentialkurven lassen sich nun die ADCs der Substanzen ermitteln, die hier den Diffusionskonstanten (D) entsprechen, da die Diffusion nicht durch Zellwände o.ä. eingeschrankt ist. Praktischer ist die logarithmierte Auftragung rechts unten, die ln(S0/S) in Abhängigkeit von b zeigt: hier entspricht D direkt der Steigung der Regressionsgeraden. Während hierfür die über das entsprechende Phantom gemittelten Intensitätswerte verwendet wurden, kann man auch für jedes Pixel ein D ermitteln. Diese Werte, in Graustufen dargestellt, entsprechen dem ADC-Map, das in der Abbildung gelb umrandet ist. Man beachte, daß für eine solche Darstellung immer mehrere Bildaufnahmen (mit unterschiedlichen b-Werten) notwendig sind. |
| Bei den bisherigen Betrachtungen wurde die Richtung des Diffusionsgradienten nicht definiert, was bei Annahme eines kugelsymmetrischen Diffusionsverhaltens aber auch nicht notwendig ist. Betrachten wir nun aber einen Fall, bei dem die Diffusion anisotrop ist, so ist die Richtung des Gradienten natürlich von entscheidender Bedeutung. Um möglichst vollständige räumliche Information zu erhalten, werden Bilder unter Verwendung von Magnetfeldgradienten in (mindestens sechs) verschiedenen Richtungen aufgenommen. Aus diesen Experimenten erhält man den sogenannten Diffusionstensor, dessen Elemente die Diffusionskonstanten für die verschiedenen Richtungen enthalten. Diese Methode, Diffusion Tensor Imaging (DTI) genannt, liefert also eine ADC-Matrix statt einer einzigen Konstante. Durch Diagonalisierung erhält man als Eigenwerte die Hauptkomponenten der Diffusion entlang der sich ebenfalls aus der Diagonalisierung ergebenden orthogonalen Eigenvektoren. |
|
Dies ist in Abb. 28 veranschaulicht, in der oben das Gleichungssystem aufgeführt ist, das sich aus der Tensorform des eindimensionalen Ansatzes S=S0·exp(-b·D) ergibt. Da es sich um ein symmetrisches Problem handelt, sind beide Tensoren, b und D, ebenfalls symmetrisch, so daß sechs verschiedene Elemente Dij existieren. Diese lassen sich durch sechs Experimente mit linear unabhängigen Gradientenrichtungen ermitteln, da man dann sechs Gleichungen für die Bestimmung der sechs Unbekannten zur Verfügung hat. D.h. aus den Experimenten mit unterschiedlichen bij bestimmt man aus der Signalintensität die Dij. Wie oben ist eine zusätzliche Messung mit |b|=0 zur Ermittlung des S0-Wertes notwendig.
Im Normalfall sind die Hauptrichtungen der Diffusion, die durch ein Ellipsoid dargestellt werden können, nicht parallel zu den Laborkoordinaten xyz, so daß die Nichtdiagonalelemente des Diffusionstensors endlich sind. Die Diagonalisierung der Matrix ist gleichbedeutend mit einer Bestimmung dieser Hauptrichtungen (Eigenvektoren), und die Diagnalelemente (Eigenwerte) sind ein Maß für die Stärke der Diffusion entlang der entsprechenden Richtungen. Im Prinzip läßt sich, analog zum oben erwähnten ADC-Map, für jedes Pixel ein solches Ellipsoid bestimmen, wobei dies offensichtlich zu einer unübersichtlichen Darstellung führt. Daher stellt man oft den Betrag der Diffusion oder eine ihrer Komponenten dar. Weit verbreitet ist auch die sogenannte Traktografie (Fiber tracking), in der man dreidimensionale Linien konstruiert, die den Richtungen der größten Eigenwerte der einzelnen Pixel folgen. |
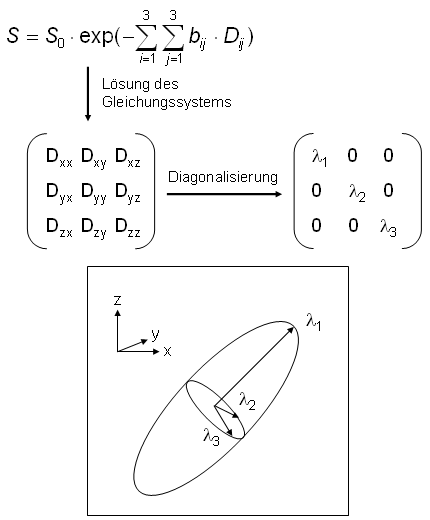 Abbildung 28 |
| Nach oben |
Literaturhinweise |
Webseiten:
|
| Nach oben |
|
|||